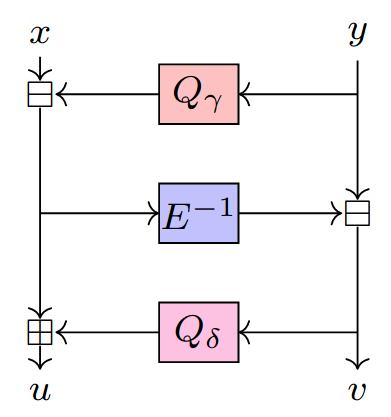
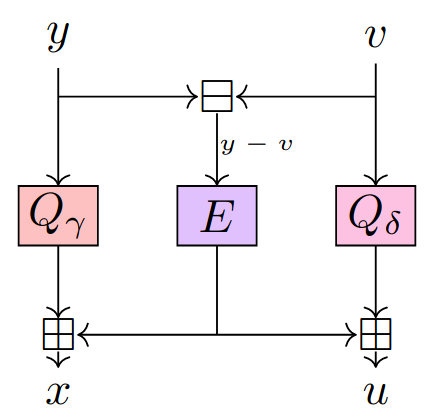
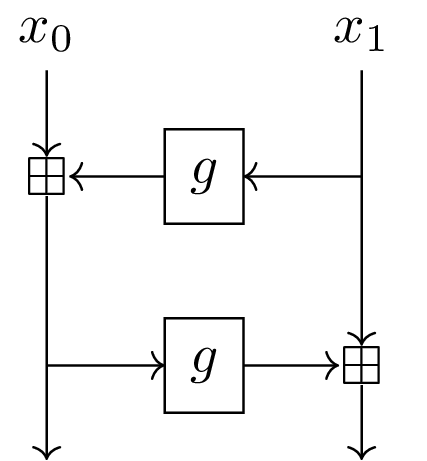
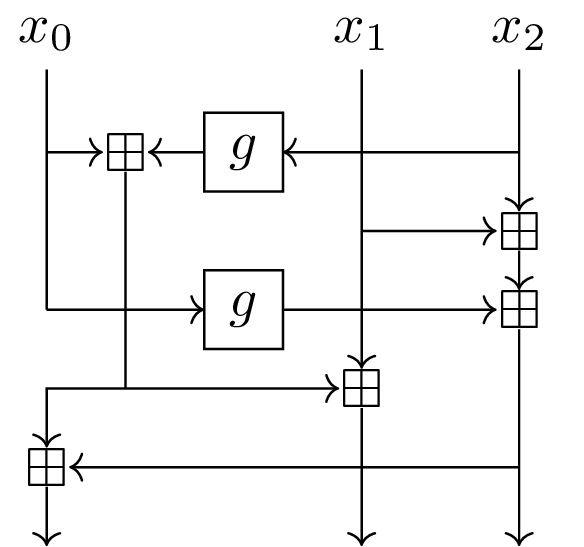
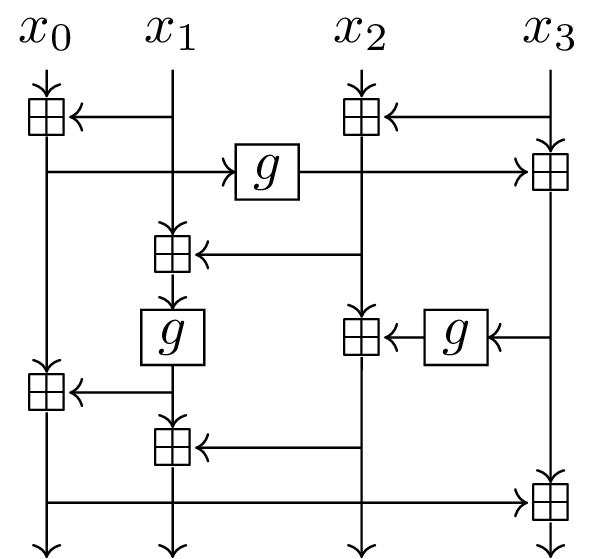
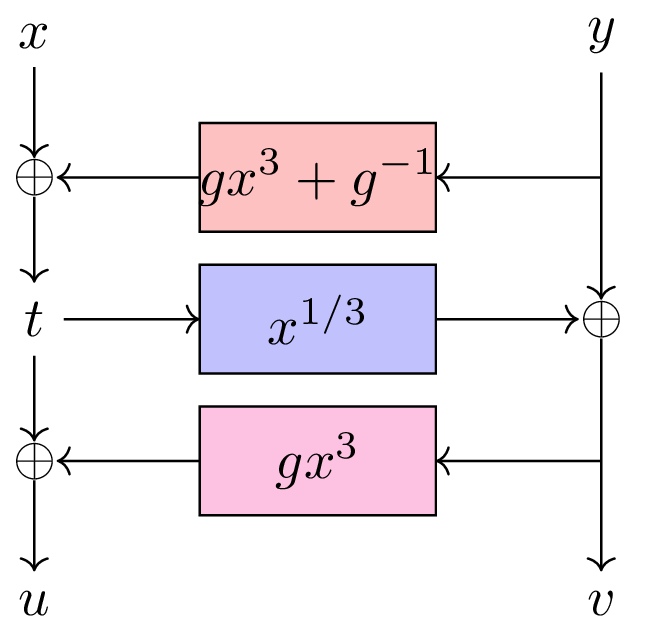
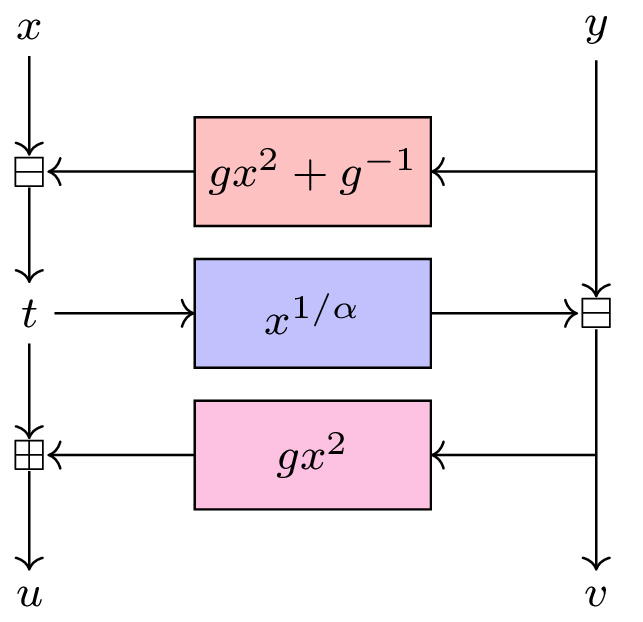
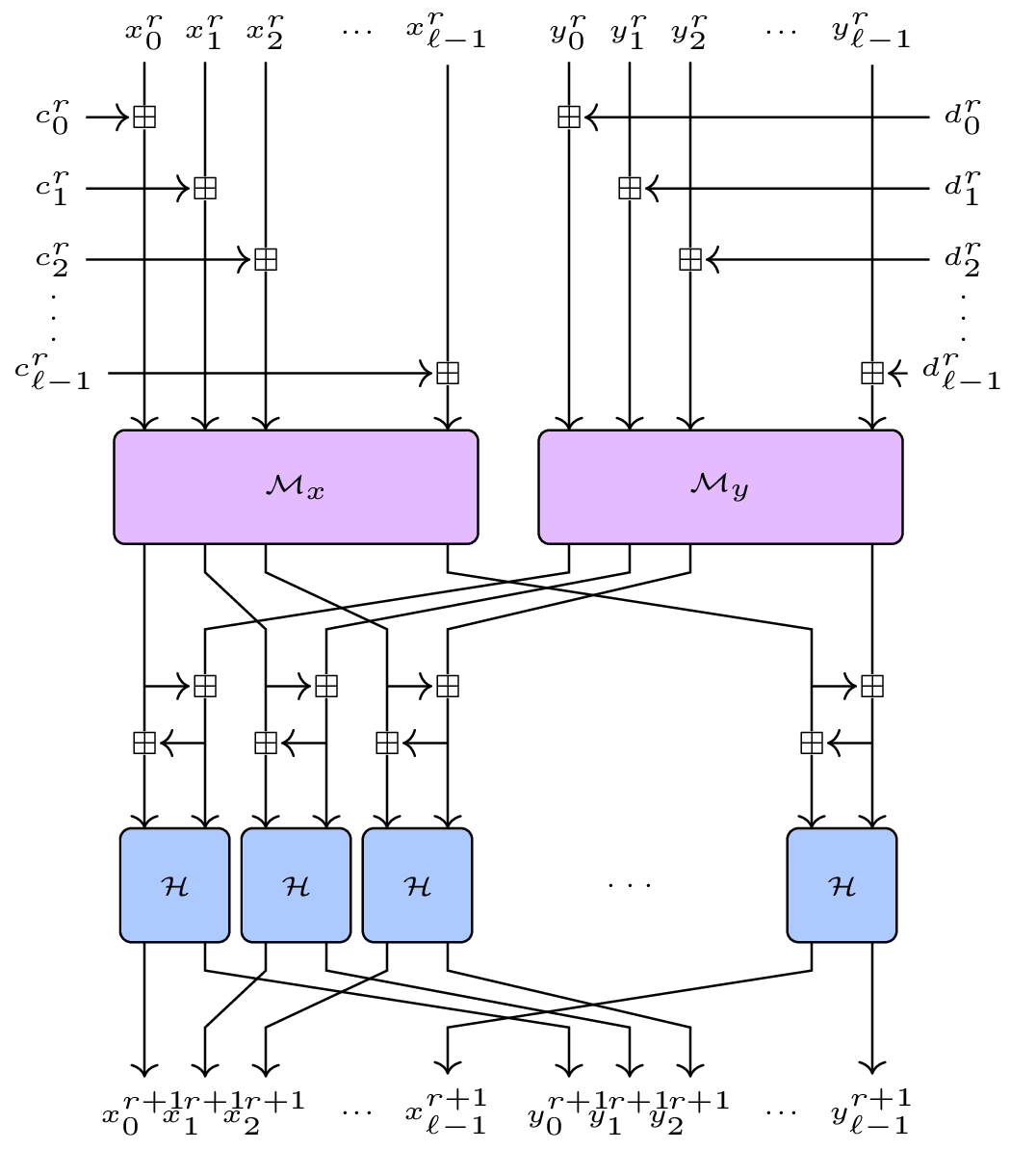
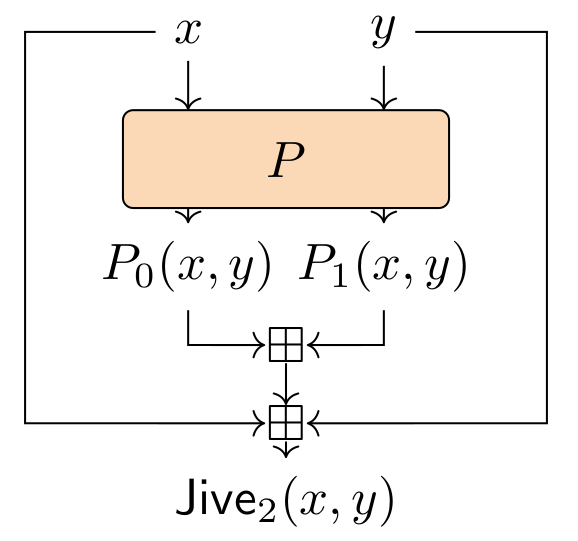
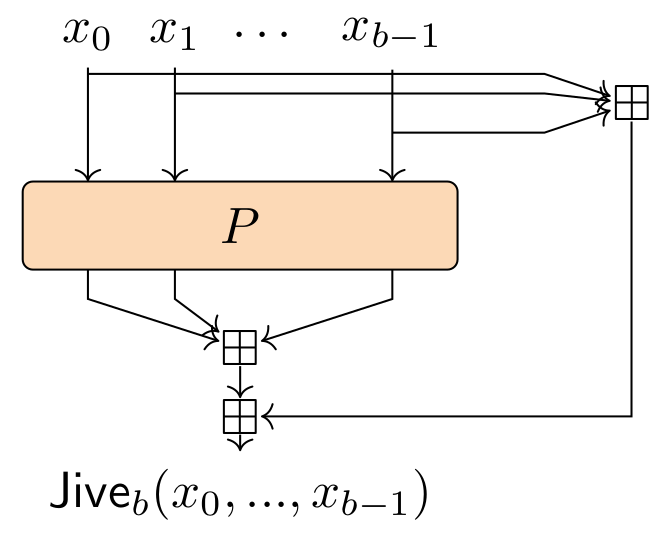
Short story
On the name
Anemoi is a family of Greek Gods of winds, then it has loose connection to butterflies which fly in the air, and that inspired the design of the Flystel. The four wind directions also symbolize the spread geographical location of the Anemoi team.

On the logo
The butterflies: one with open wings, one with closed wings refer to the open and closed Flystel. The two variants are CCZ-equivalent which is symbolized by a mirror, more precisely a sun-shaped to highlight that the closed Flystel makes the strength of Anemoi. A cloud also reminds that Anemoi represents Gods of wind.